Visual Sum of Cubes
1
2
⋅
⋅
⋅
n
1
2
2
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
n
n
1
2
2
2
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
n
n
n
This article discusses a pattern I noticed in the "visual" derivations of the formulas for 1+2+⋯+n and 12+22+⋯+n2, which led me to a similar derivation for 13+23+⋯+n3 .
∑k using two linesThere is a well-known trick for adding 1+2+⋯+n. Leaving out a bunch of + symbols, it looks like this:
k=1∑nk=12…n−1n=21(+1n2n−1……n−12n1)=21(n+1 n+1…n+1n+1)=21n(n+1)In other words, we arrange the sum as a row, then add a reverse copy of the row and multiply by 21 to keep the total the same.
Because consecutive entries increase by 1 on the first line but decrease by 1 on the reversed line, the combined entries all have the same value.
So we have n entries, all n+1, and we can simply multiply to get the total.
∑k2 using three triangles1
2
2
3
3
3
4
4
4
4
Triangle layout of 12+22+32+42
I recently came across a similar trick for the sum of squares 12+22+⋯+n2, but this time using three triangles instead of two lines!
k=1∑nk2=1
2
2
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
n
n
=31(1
2
2
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
n
n
+1
2
2
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
n
n
+1
2
2
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
n
n
)=31(2n+1
2n+1
2n+1
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
2n+1
2n+1
)=31(2n+1)2n(n+1)=61n(n+1)(2n+1)In other words, we arrange the sum as a triangle: one one (12), followed by two twos (22), and so on, down to the last row of n n (n2 ).
We then add two rotated copies of the triangle so that we have all three orientations (i.e. the 1 is at each of the three corners) and multiply by 31 to keep the total the same.
Each entry in the resulting triangle has the same value of 2n+1, and there are 1+2+⋯+n=2n(n+1) (as derived above!) entries, so we multiply just to get the sum.
∑k3 using four tetrahedraSince this trick worked for ∑k using lines and ∑k2 using triangles, I wanted to see if any shape would work for the sum of cubes 13+23+⋯+n3.
Pyramids?The easiest way to arrange ∑k3 is like a pyramid, where the top layer is a one (13), the second layer is two by two two (23), and so on, until the last layer of n -by-n n (n3). For example, for n=3:
1
2
2
2
2
3
3
3
3
3
3
3
3
3
13+23+33 pyramid layout
But pyramids aren't very symmetrical: the sides are triangles but the base is a square, so each symmetry leaves the 1 at the top and doesn't change the entries at all, which means we can't combine copies in a useful way.
Octahedra?If you double the pyramid, you get a much more symmetrical object: the octahedron. It represents 2∑k=1nk3−n3 (two pyramids, minus an nth layer since it is not doubled). For example, for n=3:
1
2
2
2
2
3
3
3
3
3
3
3
3
3
2
2
2
2
1
2⋅(13+23+33)−33 Octahedron Layout
This looks promising because we can combine rotated copies of it like we did with lines and triangles. But it only helps if the combined inputs all have the same value, and it turns out that's not the case. For n=3, for example:
1
2
2
2
2
3
3
3
...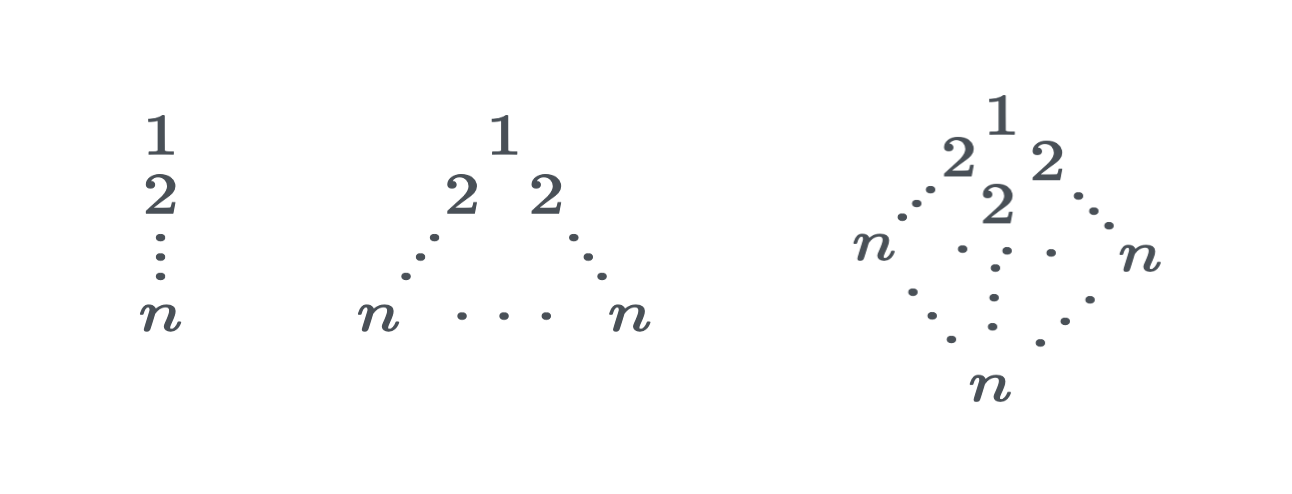
1
2
⋅
⋅
⋅
n
1
2
2
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
n
n
1
2
2
2
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
n
n
n
This article discusses a pattern I noticed in the "visual" derivations of the formulas for 1+2+⋯+n and 12+22+⋯+n2, which led me to a similar derivation for 13+23+⋯+n3 .
∑k using two linesThere is a well-known trick for adding 1+2+⋯+n. Leaving out a bunch of + symbols, it looks like this:
k=1∑nk=12…n−1n=21(+1n2n−1……n−12n1)=21(n+1 n+1…n+1n+1)=21n(n+1)In other words, we arrange the sum as a row, then add a reverse copy of the row and multiply by 21 to keep the total the same.
Because consecutive entries increase by 1 on the first line but decrease by 1 on the reversed line, the combined entries all have the same value.
So we have n entries, all n+1, and we can simply multiply to get the total.
∑k2 using three triangles1
2
2
3
3
3
4
4
4
4
Triangle layout of 12+22+32+42
I recently came across a similar trick for the sum of squares 12+22+⋯+n2, but this time using three triangles instead of two lines!
k=1∑nk2=1
2
2
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
n
n
=31(1
2
2
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
n
n
+1
2
2
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
n
n
+1
2
2
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
n
n
)=31(2n+1
2n+1
2n+1
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
⋅
2n+1
2n+1
)=31(2n+1)2n(n+1)=61n(n+1)(2n+1)In other words, we arrange the sum as a triangle: one one (12), followed by two twos (22), and so on, down to the last row of n n (n2 ).
We then add two rotated copies of the triangle so that we have all three orientations (i.e. the 1 is at each of the three corners) and multiply by 31 to keep the total the same.
Each entry in the resulting triangle has the same value of 2n+1, and there are 1+2+⋯+n=2n(n+1) (as derived above!) entries, so we multiply just to get the sum.
∑k3 using four tetrahedraSince this trick worked for ∑k using lines and ∑k2 using triangles, I wanted to see if any shape would work for the sum of cubes 13+23+⋯+n3.
Pyramids?The easiest way to arrange ∑k3 is like a pyramid, where the top layer is a one (13), the second layer is two by two two (23), and so on, until the last layer of n -by-n n (n3). For example, for n=3:
1
2
2
2
2
3
3
3
3
3
3
3
3
3
13+23+33 pyramid layout
But pyramids aren't very symmetrical: the sides are triangles but the base is a square, so each symmetry leaves the 1 at the top and doesn't change the entries at all, which means we can't combine copies in a useful way.
Octahedra?If you double the pyramid, you get a much more symmetrical object: the octahedron. It represents 2∑k=1nk3−n3 (two pyramids, minus an nth layer since it is not doubled). For example, for n=3:
1
2
2
2
2
3
3
3
3
3
3
3
3
3
2
2
2
2
1
2⋅(13+23+33)−33 Octahedron Layout
This looks promising because we can combine rotated copies of it like we did with lines and triangles. But it only helps if the combined inputs all have the same value, and it turns out that's not the case. For n=3, for example:
1
2
2
2
2
3
3
3
...What's Your Reaction?















![Three of ID's top PR executives quit ad firm Powerhouse [EXCLUSIVE]](https://variety.com/wp-content/uploads/2023/02/ID-PR-Logo.jpg?#)







